por Edgard Pereira.

O balanço de eficiência de um ato de concentração é usualmente feito utilizando-se modelos teóricos convencionais que procuram simular o ajustamento do equilíbrio do mercado pós fusão, identificando o saldo de bem-estar obtido pela contraposição entre eventual criação de poder de mercado e eficiências compensatórias.

Em um modelo de Cournot com produtos homogêneos, Farrell e Shapiro (1990)¹ mostraram que, sem a criação de sinergias substanciais, uma fusão resultaria em uma redução da quantidade produzida pela indústria e, portanto, do bem-estar. Embora os competidores usualmente reajam a um declínio da quantidade produzida pelas firmas envolvidas na fusão por intermédio de uma elevação em sua produção, o resultado líquido sobre o bem-estar seria negativo.

Se, entretanto, a fusão em um modelo de Cournot reduzir o custo marginal da firma resultante por um “montante suficiente”, ela terá um incentivo para elevar a produção após a fusão, o que resulta em preços menores e aumentos tanto da quantidade produzida pelo mercado quanto do bem-estar dos consumidores.

A derivação deste “montante suficiente” (que deixa exatamente inalterado o excedente do consumidor na comparação com a situação anterior à fusão) é apresentada a seguir, seguindo a derivação de Froeb e Werden (1998)^2.

Seja q_i a quantidade produzida pela i-ésima firma e c_i seu respectivo custo marginal de produção. Adicionalmente, denote por Q a quantidade agregada produzida pela indústria e por p o preço de mercado. A participação de mercado da i-ésima firma é dada por  s_i (= q_i / Q) e a elasticidade preço da demanda por ε (que, por convenção, é definida como positiva).

A derivação da redução percentual de custo suficiente para prevenir um aumento de preços em uma fusão envolvendo fabricantes de produtos homogêneos parte da conhecida condição necessária de primeira ordem para maximização dos lucros em um modelo de Cournot:

(1)

Esta condição de primeira ordem deve ser satisfeita tanto antes quanto após a fusão e uma fusão que não altere p também não alterará Q ou ε. Neste caso, as condições de primeira ordem das firmas não envolvidas na fusão continuam sendo satisfeitas após a operação pelos mesmos q_i’s que as satisfaziam antes. Com tanto Q quanto q_i associado às firmas não envolvidas na operação não são alterados pela fusão, a participação de mercado das firmas envolvidas na fusão após a operação deve ser igual à soma de suas participações de mercado antes da operação.

Rearranjando a equação (1), segue-se que

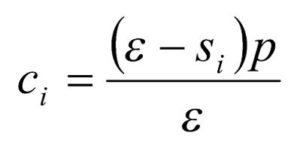
Esta equação também deve ser satisfeita pela firma resultante da fusão. Denotando as firmas envolvidas na fusão pelos subscritos j e k e substituindo a participação da firma resultante da fusão pela soma das participações das firmas j e k, obtém-se a seguinte expressão para o custo marginal da firma resultante da fusão após a operação:

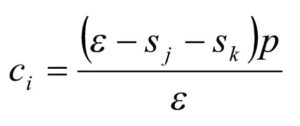
O custo marginal médio antes da fusão (ponderado pelas participações de mercado) da firma resultante da fusão é, portanto, dado por

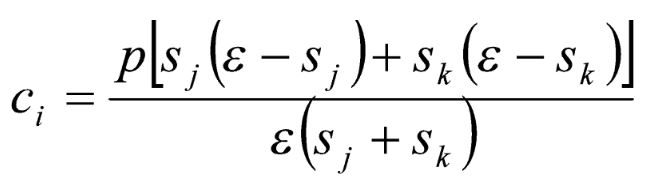
A redução proporcional no custo marginal necessária para restabelecer o preço de mercado vigente antes da operação pode ser calculada como

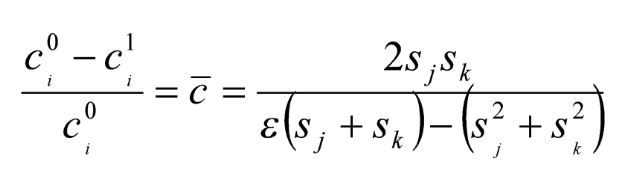
(2)

Portanto, qualquer redução de custo associada à operação superior à calculada na equação (2) garante que a fusão não resultará em aumento de preços.

Se as sinergias e ganhos de eficiência forem inferiores ao montante calculado na equação (2), a fusão acarretará uma elevação do preço de mercado.

*******

Referências:

1 – FARRELL, J., SHAPIRO, C., 1990. Horizontal mergers: an equilibrium analysis. American Economic Review 80, 107–126

2 – FROEB, L., WERDEN, G., 1998. A robust test for consumer welfare enhancing mergers among sellers of a homogeneous product. Economics Letters 58, issue 3, 367-369

Comentários:

Acesse o post do artigo no LinkedIn.

Compartilhe em sua rede: